You’re presenting project timelines to stakeholders next week. Engineering says “probably 8 weeks,” marketing estimates “6 to 10 weeks,” and your gut says “add a buffer.”
For the PMP exam, that uncertainty isn’t handled with guesswork — it’s handled with Monte Carlo analysis. This quantitative risk analysis technique is used to model uncertainty in project schedules and costs. Instead of producing a single finish date or budget, it shows the probability of different outcomes, helping project managers make risk-informed decisions.
In this guide, you’ll learn how Monte Carlo analysis is tested on the PMP exam, how it fits into quantitative risk analysis, and how to interpret probability results like confidence levels and S-curves — without doing any math.
Try monday work managementKey takeaways
- Monte Carlo analysis models schedule and cost uncertainty using probability distributions rather than single-point estimates.
- PMP candidates must understand when to use Monte Carlo analysis and how to interpret confidence levels like P50, P80, and P90.
- The technique supports quantitative risk analysis by revealing the likelihood of meeting specific deadlines or budgets.
- Monte Carlo simulation helps project managers communicate risk tolerance clearly to stakeholders.
What is Monte Carlo analysis in project management?
Monte Carlo analysis is a simulation technique that models uncertainty by running thousands of possible project scenarios. Each simulation randomly selects values for uncertain variables — such as task duration, cost, or risk impact — based on defined probability distributions.
Instead of asking, “When will this project finish?” Monte Carlo analysis answers a more useful question: “What is the probability of finishing by a specific date or within a specific budget?”
As the simulation runs, results are aggregated into probability distributions that show confidence levels for different outcomes. This allows project managers to evaluate schedule and cost risk using data rather than single-point estimates.
Core components of Monte Carlo analysis
- Input variables: Uncertain elements such as task durations, costs, or resource availability
- Probability distributions: Models describing how likely different values are for each variable
- Iterations: Thousands of simulation runs that generate possible project outcomes
- Outputs: Probability curves, confidence levels, and percentile results (P50, P80, P90)
For example, a task estimated at 30 days (optimistic), 40 days (most likely), and 60 days (pessimistic) might be modeled using a triangular distribution. After thousands of simulations, the results may show a 50% chance of finishing within 42 days, an 80% chance within 48 days, and a 95% chance within 55 days.
Monte Carlo vs. deterministic project analysis
Deterministic planning techniques use fixed values to calculate a single project outcome. While useful for baseline planning, they don’t account for how uncertainty compounds across multiple activities.
- Critical Path Method (CPM): Uses fixed task durations to calculate a single project finish date
- Program Evaluation and Review Technique (PERT): Uses weighted averages of optimistic, most likely, and pessimistic estimates but still produces one expected duration
Monte Carlo analysis differs by modeling uncertainty directly. It evaluates how multiple uncertain variables interact, revealing the probability of meeting specific schedule or cost targets.
A project with several activities — each carrying moderate risk — may appear manageable using deterministic methods. Monte Carlo simulation exposes how those risks combine, often showing a much higher likelihood of delay or overrun than individual estimates suggest.
| Dimension | Deterministic methods | Monte Carlo simulation |
|---|---|---|
| Output type | Single values | Probability distributions |
| Uncertainty handling | Point estimates or weighted averages | Full probability ranges |
| Risk visibility | Shows critical paths | Reveals likelihood of meeting specific targets |
| Complexity | Straightforward calculations | Requires computational power for thousands of iterations |
| Decision support | Answers “what’s the plan?” | Answers “what are the odds?” |
Why Monte Carlo analysis matters for the PMP exam
Monte Carlo analysis supports risk-based decision making, a core PMP competency. It is most closely associated with the Perform Quantitative Risk Analysis process and is commonly used for schedule and cost risk analysis.
The PMP exam does not test Monte Carlo calculations. Instead, it evaluates whether candidates understand:
- When Monte Carlo analysis is appropriate
- How to interpret probability-based results
- How to communicate confidence levels and risk tolerance
When an exam question emphasizes combined uncertainty, confidence levels, or probability of meeting a target, Monte Carlo analysis is typically the correct technique.
Where Monte Carlo appears in the PMP exam
The technique also connects to Project Schedule Management through schedule risk analysis and the “Develop Schedule” process. When the exam asks about techniques for analyzing schedule uncertainty or determining appropriate contingency reserves, Monte Carlo simulation is often the correct answer.
Exam blueprint connections span multiple knowledge areas:
- Project Risk Management: Primary tool for quantitative risk analysis
- Project Schedule Management: Analyzes schedule uncertainty and determines reserves
- Project Cost Management: Models cost uncertainty and supports contingency calculations
- Project Integration Management: Informs decisions through probability-based forecasting
- Agile Practice Guide: Supports release planning and sprint forecasting
Essential Monte Carlo concepts for test success
PMP candidates must understand that Monte Carlo simulation uses probability distributions to model uncertainty, runs multiple iterations to generate outcome distributions, and produces probability curves showing confidence levels for project objectives.
Key terminology includes “iteration” (a single simulation run), “probability distribution” (mathematical description of variable uncertainty), “confidence level” (probability of achieving a specific outcome), and “S-curve” (cumulative probability curve showing likelihood of finishing by various dates).
Critical concepts for exam success include:
- Purpose: Models combined uncertainty effects and reveals probability distributions
- Inputs: Probability distributions for uncertain variables
- Process: Random sampling, multiple iterations, result aggregation
- Outputs: Probability curves, confidence levels, risk exposure metrics
- Interpretation: P50 is median outcome, P80/P90 are conservative estimates
Common Monte Carlo exam scenarios
Exam questions often present a project manager facing schedule uncertainty across multiple critical tasks. The scenario describes 3-point estimates for key activities and asks which technique best analyzes the combined schedule risk. Monte Carlo simulation is the correct answer when the question emphasizes modeling combined uncertainty or determining confidence levels.
Another common scenario involves stakeholder communication about project timelines. The question might describe a project manager who has completed Monte Carlo analysis and must explain results to executives. Correct answers emphasize presenting probability ranges rather than single-point estimates.
How Monte Carlo simulation works in 5 steps
Monte Carlo takes all those “maybe” and “probably” estimates and turns them into actual numbers you can plan with — through these 5 straightforward steps. Each step builds on the previous one, moving from identifying what’s uncertain to generating actionable insights. The methodology remains consistent whether analyzing a 3-month software release or a 5-year infrastructure program.
The complexity and number of variables scale with project size, but the core process stays the same. Understanding this structured approach helps project managers implement Monte Carlo analysis effectively and interpret results accurately.
| Step | Key activities | Primary output | Common challenges |
|---|---|---|---|
| Variable identification | Define uncertain elements, assess impact | List of critical variables | Distinguishing significant from trivial uncertainties |
| Distribution definition | Assign probability curves to variables | Mathematical models of uncertainty | Selecting appropriate distribution types |
| Simulation execution | Run thousands of iterations | Raw scenario data | Determining sufficient iteration count |
| Results analysis | Interpret probability curves | Confidence intervals and risk metrics | Translating statistics into business language |
| Insight generation | Convert data into decisions | Actionable recommendations | Balancing precision with practical constraints |
Step 1: Identify project variables and uncertainties
The first step requires systematic identification of every project element containing meaningful uncertainty. This goes beyond obvious risks like weather delays or vendor performance. Focus on variables that significantly impact project objectives and contain genuine unpredictability.
Focus your modeling efforts on variables with significant unpredictability, such as a task that could take anywhere from 2 days to 2 weeks.
Effective variable identification considers multiple categories of uncertainty:
- Schedule uncertainties: Task durations, dependency relationships, resource availability windows, approval cycle times
- Cost uncertainties: Material prices, labor rates, currency fluctuations, scope change impacts
- Resource uncertainties: Team member availability, skill level variations, contractor reliability, equipment uptime
- External uncertainties: Regulatory approval timelines, market condition changes, technology evolution, stakeholder decision speeds
Document each variable with its potential range and the factors driving its uncertainty. A software testing phase might vary based on defect discovery rates, tester availability, and environment stability.
Step 2: Define probability distributions for each variable
Each identified variable needs a probability distribution describing how likely different values are. The most common distributions in project management are triangular, normal, and uniform. Triangular distributions work well for task duration estimates where you have optimistic, realistic, and pessimistic scenarios.
A development task might have a triangular distribution with 5 days (optimistic), 8 days (most likely), and 15 days (pessimistic).
Selecting the right distribution type significantly affects simulation accuracy:
- Triangular: Use for 3-point estimates common in project planning
- Normal: Apply to variables affected by many independent factors
- Lognormal: Choose for variables that can’t go below zero but have long positive tails
- Uniform: Select when all values in a range are equally probable
- Beta: Employ for variables bounded by minimum and maximum with flexible shapes
Historical data provides the best foundation for distribution parameters. If past projects show testing phases ranging from 12 to 28 days with an average of 18 days, those numbers inform your distribution.
Step 3: Generate random scenarios through simulation
Simulation execution involves selecting random values from each probability distribution across thousands of iterations to generate possible project outcomes. More likely values appear more frequently, creating realistic probability distributions for schedule or cost results.
Key considerations include:
- Iteration count: 5,000 iterations provide reasonable accuracy for most projects
- Correlation modeling: Define relationships between variables to prevent unrealistic combinations
- Convergence testing: Verify that additional iterations don’t significantly change results
Step 4: Analyze probability curves and confidence levels
The simulation output is a probability distribution showing how likely different project outcomes are. For schedule analysis, this appears as a cumulative probability curve (S-curve) where the x-axis shows project duration and the y-axis shows the probability of finishing by that date.
Reading these curves requires understanding confidence levels. If the curve shows 70% probability of completing within 120 days, there’s also 30% probability of taking longer. Stakeholders must decide their risk tolerance.
Key probability curve insights translate statistical outputs into business decisions:
- P50 (median): The outcome with 50% confidence
- P80 (80th percentile): Conservative estimate with only 20% chance of exceeding
- P90 (90th percentile): Highly conservative estimate for projects with severe delay penalties
- Range width: Distance between P10 and P90 indicates uncertainty magnitude
- Distribution shape: Symmetrical curves indicate balanced risk
Step 5: Transform results into actionable insights
You can unlock the value of raw probability data by translating it into decisions and actions. This final step converts statistical outputs into project management strategies.
Schedule insights might reveal that while the P50 completion date is June 15, the P80 date is July 10. This 25-day gap indicates significant schedule risk. You can then investigate which variables drive this uncertainty and focus mitigation efforts there.
Cost analysis might show a P50 budget of $2.8 million but a P90 budget of $3.4 million. This $600,000 variance informs contingency reserve decisions. Rather than setting aside an arbitrary 10% buffer, you can justify a specific reserve amount based on the desired confidence level.
Try monday work management4 powerful applications of Monte Carlo in risk management
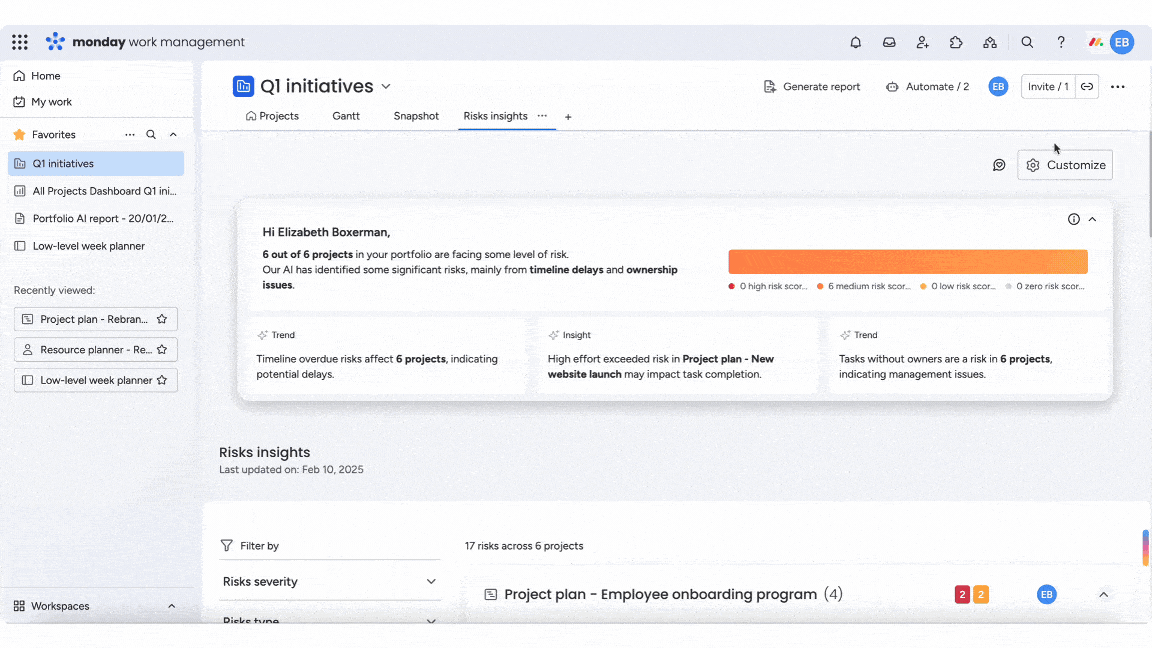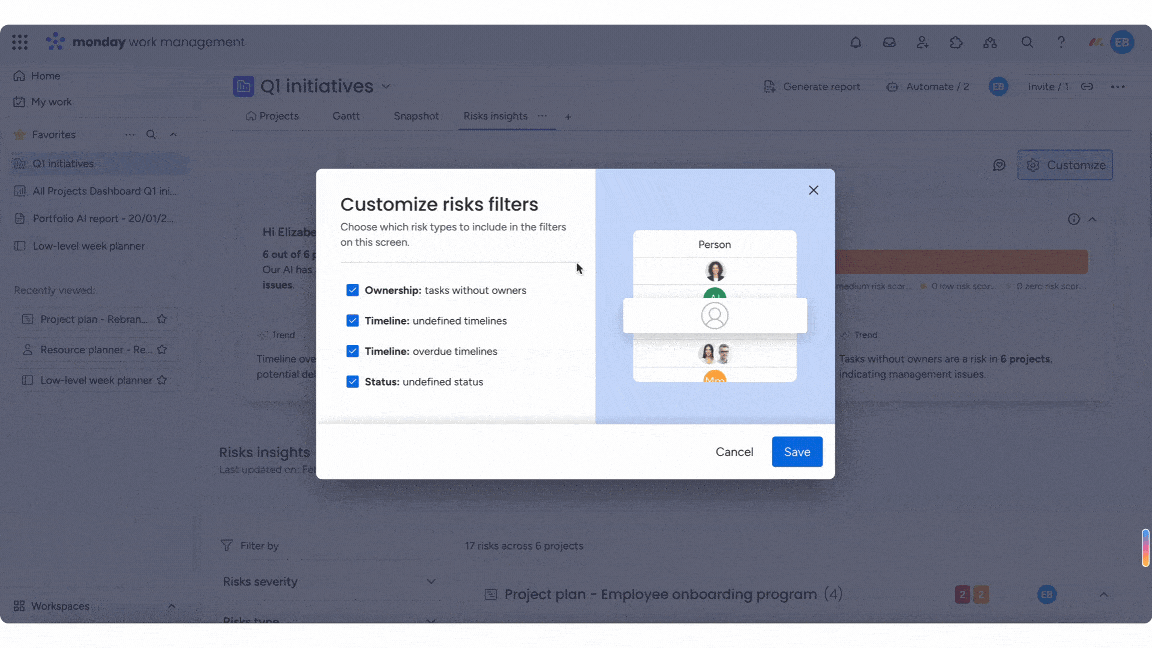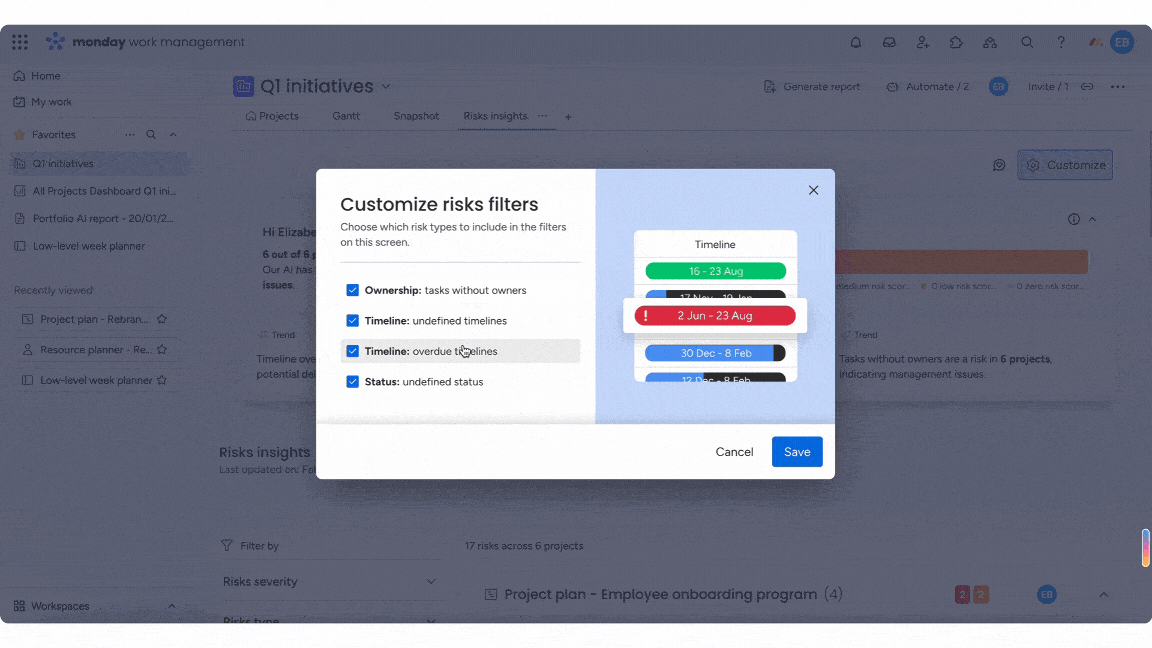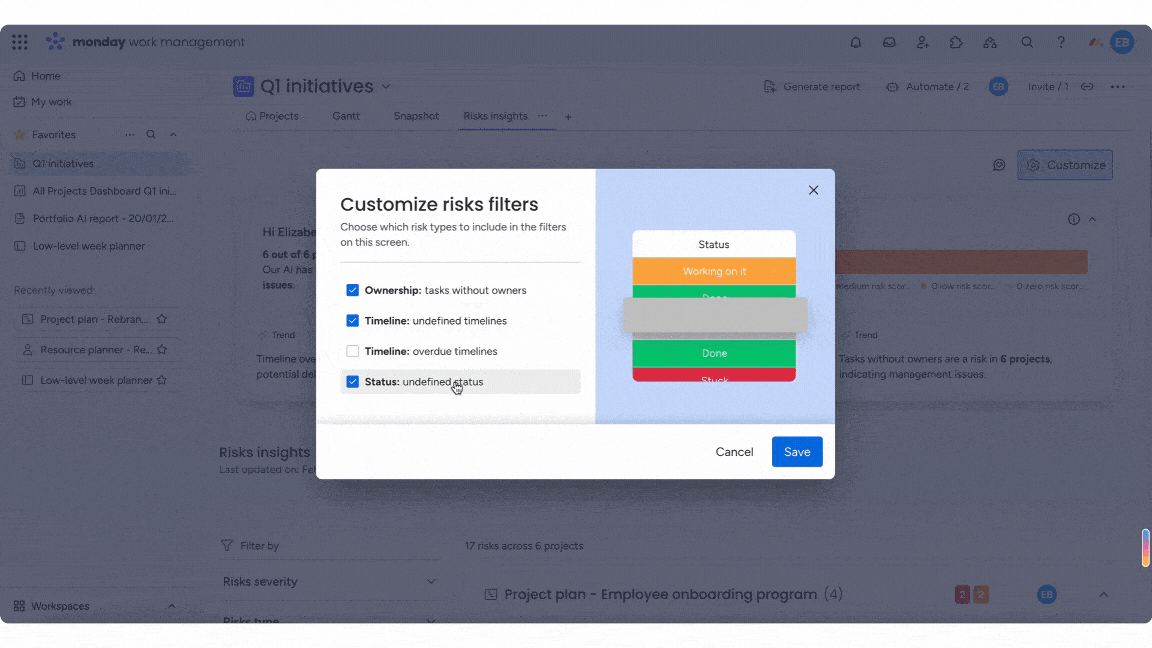
Monte Carlo analysis extends far beyond simple schedule or cost estimation. The technique’s ability to model complex interactions between multiple uncertain variables makes it valuable across the full spectrum of project risk management. These applications demonstrate how probabilistic thinking transforms traditional project management approaches.
Each application addresses specific challenges that deterministic methods struggle to handle effectively. Understanding these examples helps project managers identify when Monte Carlo analysis provides the most value.
1. Project schedule risk analysis
Monte Carlo simulation models uncertainty in task durations, resource availability, and dependency relationships to reveal the probability distribution of project completion dates. A project might have a P50 completion date of May 15, a P80 date of June 1, and a P90 date of June 12.
This probability range helps project managers:
- Set realistic commitments: Choose confidence levels that match stakeholder risk tolerance
- Size schedule reserves: Calculate buffer time based on statistical analysis rather than guesswork
- Identify critical uncertainties: Focus mitigation efforts on variables that most impact completion probability
2. Cost estimation and budget reliability
Monte Carlo analysis transforms cost estimates from single-point predictions into probability distributions reflecting real-world uncertainty. The technique models variations in material costs, labor rates, equipment expenses, and indirect costs.
A construction project might have a P50 cost of $8.2 million but a P80 cost of $9.1 million, indicating substantial cost risk. This analysis supports:
- Contingency planning: Justify reserve amounts with statistical backing
- Budget approval: Present realistic cost ranges to stakeholders
- Financial risk assessment: Quantify exposure to cost overruns
3. Portfolio-level risk aggregation
Monte Carlo simulation aggregates uncertainty across multiple projects to reveal portfolio-level risk exposure. The technique models correlations between projects to show realistic portfolio outcomes.
An organization running 20 projects might expect 18 to finish on time based on individual P80 estimates, but portfolio management analysis might reveal only 14 on-time completions are probable due to shared resource constraints. This enables:
- Portfolio optimization: Balance risk across multiple initiatives
- Resource allocation: Account for cross-project dependencies
- Strategic planning: Set realistic expectations for portfolio delivery
4. Scope change impact assessment
Monte Carlo simulation evaluates how proposed scope changes affect project risk profiles by modeling the uncertainty those changes introduce. A change estimated at 3 weeks might have a P50 impact of 3.2 weeks but a P80 impact of 4.5 weeks due to uncertainty in requirements, technical complexity, and integration effort.
Scope change analysis supports:
- Change approval decisions: Present realistic impact ranges to change control boards
- Timeline adjustments: Update project schedules with probabilistic change impacts
- Risk communication: Help stakeholders understand uncertainty introduced by changes
Use monday work management to support Monte Carlo-style risk analysis
Modern project management platforms can support Monte Carlo-style analysis by capturing uncertainty, modeling scenarios, and updating forecasts as data changes. Rather than relying on manual spreadsheets or specialized software, teams can integrate probabilistic thinking directly into their planning workflows.
Platforms like monday work management help teams:
- Capture 3-point estimates for uncertain tasks
- Visualize probability ranges and confidence levels
- Update forecasts dynamically as project conditions change
For PMP candidates, it’s important to understand that tools support Monte Carlo analysis — but the exam focuses on when and why to use the technique, not the software itself.
Make Monte Carlo analysis work for your projects
Teams that embrace Monte Carlo stop guessing and start knowing. They spot risks earlier, forecast with confidence, and earn stakeholder trust by backing up timelines with data instead of optimism. The methodology scales from individual projects to enterprise portfolios, providing consistent risk assessment across all organizational levels.
With monday work management, teams can incorporate probabilistic thinking into everyday project planning workflows. For PMP candidates, it’s important to understand that tools can support Monte Carlo-style analysis — but the exam focuses on when and why to use the technique, not the software itself.
Try monday work managementFAQs
What does a Monte Carlo analysis tell you?
Monte Carlo analysis tells you the probability distribution of project outcomes, showing not just what might happen but how likely each outcome is. It answers questions like "What's the probability of finishing by June 30?" or "What budget gives us 90% confidence?" rather than providing single-point estimates.
What is Monte Carlo analysis in Agile project management?
Monte Carlo analysis in Agile project management models uncertainty in sprint velocity, story point completion rates, and release timing. It helps teams forecast release dates with confidence levels, plan capacity more realistically, and communicate probability-based timelines to stakeholders rather than making deterministic commitments.
Can AI platforms run Monte Carlo simulations automatically?
AI platforms can run Monte Carlo simulations automatically by fitting probability distributions to historical data, generating realistic scenarios accounting for variable correlations, and updating simulations continuously as project data changes. This automation makes Monte Carlo analysis accessible without requiring statistical expertise or manual calculation.
How many iterations should a Monte Carlo simulation include?
A Monte Carlo simulation should include 5,000 to 10,000 iterations for most project applications, which provides sufficient accuracy for decision-making. More complex programs with many variables might use 20,000 iterations, while simpler projects can achieve reasonable results with 3,000 iterations.
Is Monte Carlo analysis required for PMP certification?
Monte Carlo analysis is not required to pass the PMP exam, but candidates must understand the concept, know when it's appropriate to use, and be able to interpret basic probability curves. The exam tests conceptual knowledge rather than calculation ability, focusing on Monte Carlo's role in quantitative risk analysis.
